
- #LOOP IN R FOR STOCKS RETURN HOW TO#
- #LOOP IN R FOR STOCKS RETURN CODE#
- #LOOP IN R FOR STOCKS RETURN DOWNLOAD#
Function tapply returns a listĪnd sorts its elements using the names. For that, we will useįunction tapply to calculate the returns of each stock. Store them in the same dataframe with the prices. Remember that you always lose the first observation (row)įollowing up, we will first calculate the returns of all assets and Therefore, it is necessary that returns and prices have the The next steps we will column bind the vector of returns in the priceĭataframe.
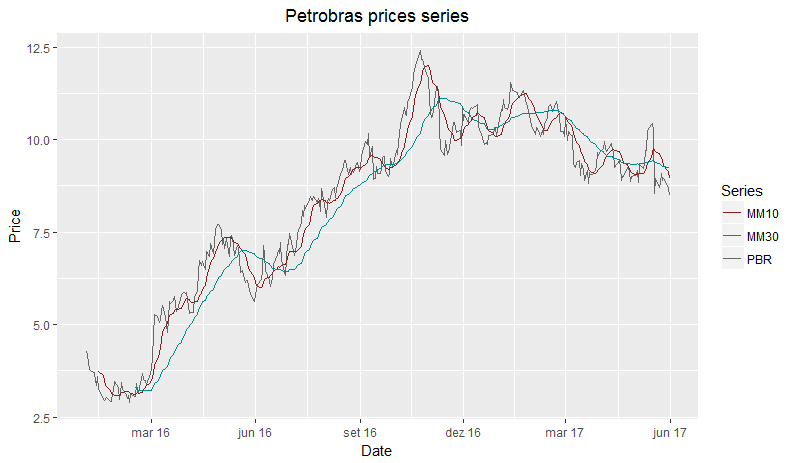
Notice that I used a NA for the first element of the return vector. Write a simple function that, given a vector of prices, outputs a vectorĪrit.ret <- c(NA, log(p/p)) In order to calculate daily returns for each stock, the first step is to In practice, though, it makes very little difference. Returns are more used in research since they have some special We have twoĬhoices here, arithmetic or logarithmic returns. Regression, however, returns (and not prices) are used. In the previous step we downloaded prices from yahoo finance. Splits and inplits are already taken into account and the result is a Artificial effects in the dataset such as ex-dividend prices, This is one of theĪdvantages of working with adjusted (and not closing) prices from yahooįinance. P <- p + facet_wrap(~ticker, scales = 'free')Īgain, we see that all prices seems to be Ok. P <- ggplot(df.stocks, aes(x=ref.date, y=price.adjusted)) Now, lets check if everything went well with the import process. # Downloading Data for ^GSPC from yahoo (11|11) - Good stuff! # Downloading Data for CAH from yahoo (10|11) - Good job! # Downloading Data for LH from yahoo (9|11) - Nice! # Downloading Data for FB from yahoo (8|11) - Nice! # Downloading Data for SRE from yahoo (7|11) - Got it! # Downloading Data for IR from yahoo (6|11) - Good job! # Downloading Data for HST from yahoo (5|11) - Good job! # Downloading Data for AAL from yahoo (4|11) - Nice! # Downloading Data for LLY from yahoo (3|11) - Got it! # Downloading Data for CCI from yahoo (2|11) - Well done! # Downloading Data for DUK from yahoo (1|11) - Good stuff! # tickers = DUK, CCI, LLY, AAL, HST, IR, SRE, FB, LH, CAH, ^GSPC L.out <- BatchGetSymbols(tickers = my.tickers, My.tickers <- c(sample(GetSP500Stocks()$tickers,n.chosen.stocks), N.chosen.stocks <- 10 # can't be higher than 505 BatchGetSymbols: Downloads and Organizes Financial Data for Multiple Tickers. # Thank you for using BatchGetSymbols! If applicable, please use the following citation in your research report.
#LOOP IN R FOR STOCKS RETURN CODE#
Runs the code available here will get the exact same results. Will also add the ticker ^GSPC, which belongs to the SP500 index. In this example we willĭownload data for 10 stocks selected randomly from the SP500 index. I’m a bit biased, but I really like using package BatchGetSymbols toĭownload financial data from yahoo finance.
#LOOP IN R FOR STOCKS RETURN DOWNLOAD#
In this post I will download some data from the US market, make someĪdjustments to the resulting dataframe and discuss three ways toĬalculate the betas of several stocks.
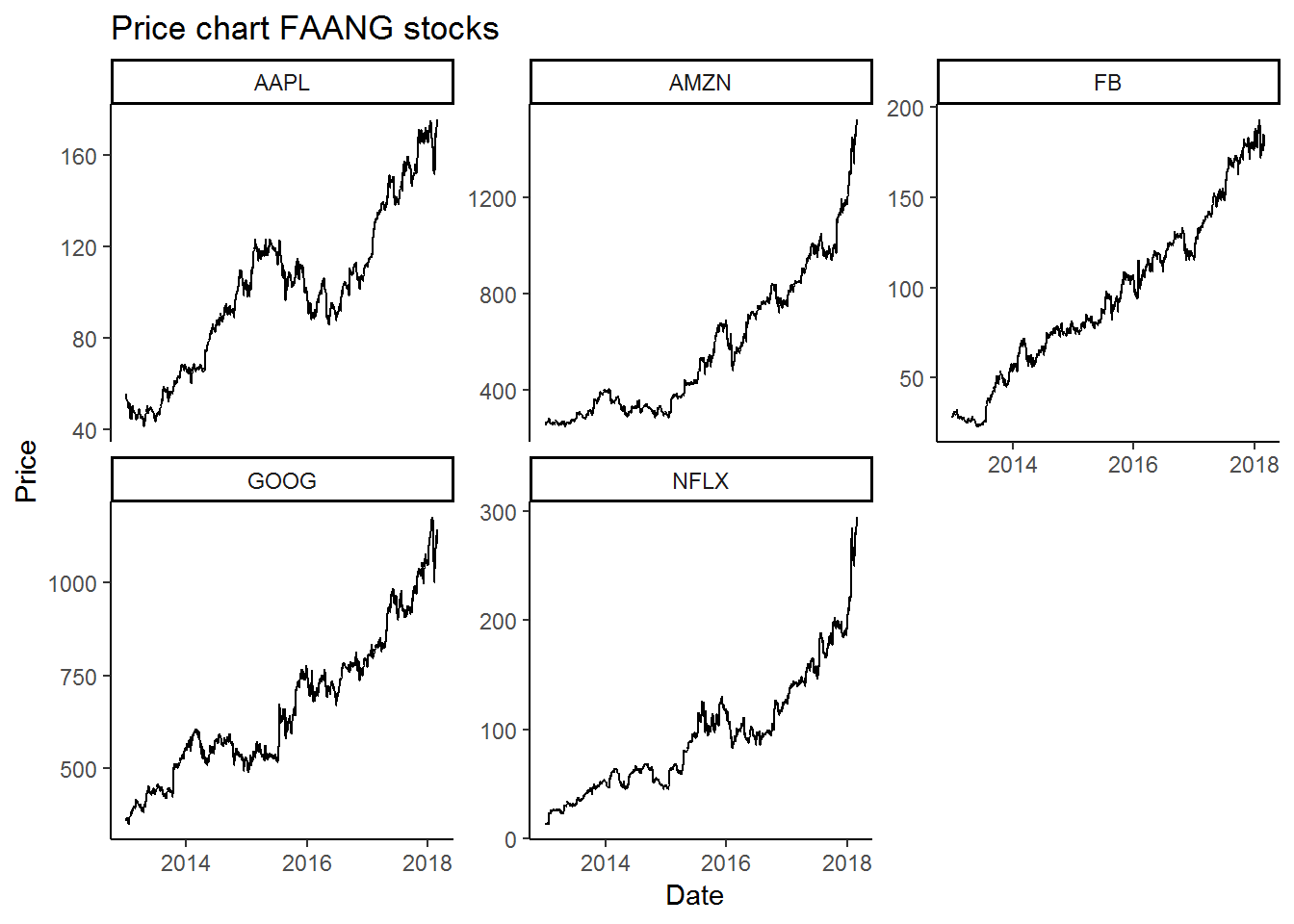
Where R really shines in comparison to simpler programs such as Excel. Procedure for more than one stock, some programming is needed.

#LOOP IN R FOR STOCKS RETURN HOW TO#
Learned in class how to estimate one model. This is where students usually have problems, as they only You want to calculate the systematic risk for a large number of The problem here is that, usually, you don’t want the beta of a single Market index, you can easily find the stock’s beta by calculating theĭaily returns and estimating the market model. Vector of prices for a stock and another vector of prices for the local Minimizing the sum of squared errors of the model. R M, t is the return of the market index, α is theĬonstant (also called Jensen’s alphas) and, finally, β is the measure Where R t is the return of the stock at time t, In the quantitative side, we can formulate the market model as: Returns, that is, stocks with higher betas should present, collectively, Summing up, theĬAPM model predicts that betas have a linear relationship to expected Returns, rational investors and frictionless market. Model equation by assuming several conditions such as Normal distributed Relates expected return and systematic risk. Vector of a stock and the explanatory variable is the return vector of aĭiversified local market index, such as SP500 (US), FTSE (UK), Ibovespaįrom the academic side, the calculation of beta is part of a (very)įamous asset pricing model, CAPM – Capital Asset Pricing Model, that One of the first examples about using linear regression models inįinance is the calculation of betas, the so called market model.Ĭoefficient beta is a measure of systematic risk and it is calculated byĮstimating a linear model where the dependent variable is the return A comparison between using a loop, function by and the package dplyr –


 0 kommentar(er)
0 kommentar(er)
